Uvidíme sa v 4D - matematická demonštrácia štvrtej dimenzie

Materiál od Alexandru Lamba

Problém štúdia viacrozmerných telies nie je nový. Aj keď konkrétny svet, v ktorom žijeme, má iba tri merateľné materiálne rozmery, samotný vesmír je trojrozmerný, koncepty ako „multiverse“ alebo „n-dimenzionálne priestory“ boli vyvinuté vo svete umenia aj v exaktných vedách. mohol povedať, a to v súvislosti s mystikou.

Vo svete umenia sa SF zďaleka najviac zaujíma o multidimenzionálnosť, aj keď časom to nebola jedna z jeho obľúbených tém, ale iba užitočný koncept. Najvýhodnejším spôsobom cestovania vesmírom v SF teda zostáva „červia diera“, skratka cez „záhyb“ trojrozmerného priestoru vo multidimenzionálnom multiverze, ale toto je iba prenosový režim, rafinovanosť, nie problém. študovať sama.

Je viacpriestorová geometria

Ak sa pozrieme retrospektívne, čaká nás dvojité prekvapenie, keď zistíme, že tento koncept existuje od roku 1666, keď sa objavil s príbehom „The Blazing World“ od Margaret Cavendish, príbehom, v ktorom spája Zem s iným svetom. súhvezdí na oblohe a oveľa bližšie k problematike, ktorej sa budeme venovať nižšie, a to prechodu medzi rôznymi svetmi v množstve ortogonálnych rozmerov, predstavil v roku 1884 Edwin Abbott Abbott prostredníctvom svojho dokumentu „Flatland, A Romance Of Many Dimensions “, dielo, ktoré zosobňuje ploché geometrické postavy a stavia ich tvárou v tvár telesám geometrie v priestore.

Aj keď je to zaujímavý a iba z tohto pohľadu, predmetný príbeh chce opäť ohromiť, keď vyvolá otázku: „ale ďalej, čo to bude?“. Presne na túto otázku by som sa chcel zamerať na nasledujúce, najpraktickejšie a „vizuálne“ možné. Pretože, či už ide o literatúru, fyziku alebo geometriu, ktorú si nedokážeme predstaviť, bude pre nás veľmi ťažké úplne pochopiť. A to aj napriek tomu, že svet vedy dlho akceptoval skutočnosť, že samotné vnímanie nemôže definovať realitu.

Až donedávna, keď pojem „tesseract“ začal naberať na sile, aj keď rovnice entít definované v n-dimenzionálnych priestoroch boli v analytickej geometrii bagatelizované, je kuriózne, že problém ich vizuálneho zobrazenia sa nikdy príliš netešil. veľký záujem. Ale akonáhle pripustíme, že niektoré javy sa odohrávajú nad naše možnosti vnímania, a aby sme ich aspoň čiastočne dokázali stráviť, veľmi nám pomôže vizuálna forma znázornenia (nie nadarmo sa hovorí, že „obraz robí tisíc slovami “) sa stáva zrejmou potreba zastupovať orgány s viac ako tromi rozmermi.

Oko sa vyrieši za zlomok sekundy, ak je ponúkané v známej podobe, ktorej analyzovanie by mysle trvalo možno hodiny, iba z rovníc alebo reťazcov. Dokazuje to samotný koncept grafu funkcie, ktorý sa používa nielen v matematike, ale aj v ekonómii alebo spoločenských vedách. V takom prípade, ak sa vrátime k geometrii, nemyslím si, že by sa čudovalo, že grafické znázornenie je základom porozumenia.

Jednoduchý obraz je samozrejme nepresný a nedostatočný, je však nevyhnutný pri riešení akýchkoľvek problémov v tejto oblasti matematiky. Presne o týchto grafických znázorneniach budeme hovoriť ďalej, keď sa pokúsime vizualizovať, čo je za naším trojrozmerným priestorom, ako nás Edwin Abbott Abbott žiada od devätnásteho storočia. Urobíme to isté, čo anglický učiteľ vo svojom literárnom prístupe (nazývanom tiež matematická fikcia), počnúc vývojom dvojrozmernej až trojrozmernej.

Vizualizácia hyperpriestoru

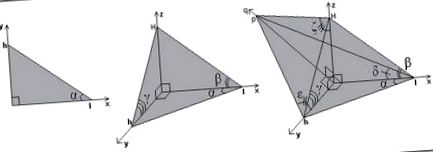
Najskôr zafixujeme súradnicové systémy pre referenciu, počnúc nakreslením trojrozmerného systému karteziánskych osí na papieri. Ako je známe, plán (napríklad list papiera) má iba dva rozmery. To nám však nikdy nebránilo kresliť a rozpoznávať trojrozmerné telá, však? Ako presne to robíme? No, veľmi jednoduché: oklamať oko, prinútiť ich myslieť si, že určité uhly sú správne, aj keď nie. Rovnakým spôsobom sa ich pokúsime oklamať, aby videli štvorrozmerné telá.

Ďalej vidíme, ako pridaním osi pod určitým uhlom (os z) k súradnicovému rovinnému systému x-y získame falošný trojrozmerný systém (so všetkými tromi osami vždy kolmými), ktorý však oko ako také bez problémov akceptuje. Samotné ľudské videnie je ploché, sietnica je usporiadaná na povrchu a hĺbka sa nevníma priamo, ale prostredníctvom triangulácie a ... „zážitku“.

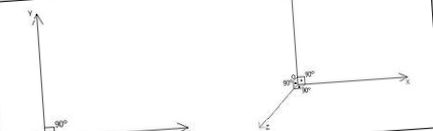
Oko vidí ploché obrazy, ktoré sa na základe predchádzajúcich poznatkov o realite transponujú do vesmíru. Je to práve tento nedokonalý mechanizmus videnia, ktorý nám môže pomôcť prinútiť ho presahovať to, čo je skutočné. Pretože oko môže byť presvedčené, že sa os z odchyľuje od roviny, môže byť tiež presvedčené, že štyri čiary sú kolmé, resp. Konkrétne, postupujúc vyššie, vychádzame z vesmírneho modelu systému xyz priestorových súradníc so všetkými tromi kolmými osami a pridáme štvrtú z určitého uhla, potom nútime oko vidieť ktorékoľvek dve zo štyroch osí ako navzájom kolmé.

(Aby sme ponúkli ľahko rekonštituovateľné riešenie, môžete zvoliť ľahko dostupné magnetické gule a tyče) Získame tak definovanú štvorrozmernú geometrickú entitu, ktorú budeme nazývať ďalej. hyperpriestor.

Dokážete, ak sa pokúsite, presvedčiť samého seba, že ktorékoľvek dve osi sú kolmé? Perfektné, sme na dobrej ceste! Okrem toho môžeme prinútiť oko, aby prijalo za platný taký systém osí, ktorý je nakreslený aj na papieri, pričom nakreslí dve osi skutočne kolmé na seba a ostatné uhly označí ako priame:

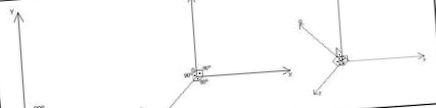
Takže tak, že pridaním osi z do roviny xy sme získali priestor xyz, ktorý má tri kolmé roviny: xy, xz a yz, pridaním ďalšej osi q do priestoru xyz, sme získali štvorrozmerný hyperpriestor xyzq so štyrmi priestormi „kolmými“ medzi oni: xyz, xyq, xzq a yzq, respektíve šesť kolmých rovín: xy, xz, xq, yz, yq a zq. Môžete si ich pozrieť? K dispozícii sú každý, vizuálne, trojrozmerné priestory, respektíve plány?

Aby sme zabezpečili, že sme nezabudli na žiadny prvok, môžeme použiť kombinatorický výpočet: keď máme počet štyroch ortogonálnych osí a vieme, že potrebujeme dve pre rovinu a tri pre priestor, problém určenia ich počtu je rovnaký ako riešenie Cn k: kde n = počet dostupných os a k = počet požadovaných osí (C4 2 = 6, v prípade plánov hyperpriestoru, C4 3 = 4, v prípade priestorov hyperpriestoru). Presne ten istý výpočet je základom pre určenie počtu rovín v trojrozmernom priestore, ale keďže je takým bežným problémom, zdá sa, že jeho riešenie je vlastné.

Teraz, keď sme definovali hyperpriestor, naplnime ho, pretože to je to, čo sme sa sem skutočne chceli dostať: prezeranie štvorrozmerné hyperbody. V tomto článku budeme spokojní s vizualizáciou tých najjednoduchších z nich, a to obdĺžnikový hyperparalipiped (brat s nerovnakými stranami hyperkocky alebo tesseract) a obdĺžnikový hypertréder. Budeme ich konštruovať na základe obdĺžnikového rovnobežnostenu, respektíve obdĺžnikového štvorstenu, rovnakým spôsobom, v akom boli posledné vyrobené na základe obdĺžnika, respektíve pravého trojuholníka.

Obdĺžniková hyperpalaleipipeded

Začnime s výstavbou hiperparalelipipedului, vychádzajúc z jednoduchého obdĺžnika v rovine x-y. Intuitívne vidíte, ako „potiahnutím“ alebo „vynásobením“ obdĺžnika pozdĺž osi z získate obdĺžnikový rovnobežnosten. Rovnakým postupom v priestore 4D „potiahneme“ rovnobežnosten pozdĺž osi q a obdĺžnikový hyperparallelip sa objaví nasledovne:

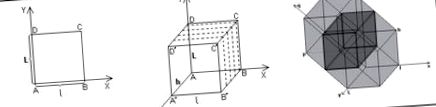
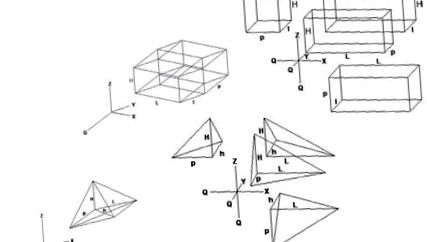
Pre jednoznačnejšiu reprezentáciu je možné vytvoriť 3D model, ako je uvedené nižšie, z dvoch rovnakých rovnobežnostenov, ktoré majú spojené rohy rovnobežných strán nakreslené pozdĺž osi q, nepravdivé kolmo na všetky ostatné:

Len čo je model vyrobený, vyzývam vás, aby ste identifikovali a „vizualizovali“ všetky obdĺžnikové rovnobežnosteny, ktoré vymedzujú tento hyperparalelipid! Uvidíte, že akonáhle presvedčíte svoje oči, aby prijali niekoľko nesprávnych pravých uhlov za správne, trojrozmerné telá, ktoré „obliekajú“ toto 4D telo, budú vyzerať rovnako normálne ako obdĺžniky v tvare rovnobežníka, ktoré obklopujú obdĺžnikový rovnobežnosten nakreslený na papier.

A pretože vedecký prístup nie je úplný bez niekoľkých rovníc, navrhujem vám analyzovať hlavné charakteristické veľkosti týchto telies pri zachovaní analógie s obdĺžnikom a obdĺžnikovým rovnobežníkom. Ktoré to sú? Pre obdĺžnik (plochá postava) - plocha a obvod a pre rovnobežnosten (trojrozmerné telo) - objem a bočná plocha.

Všimli sme si, že obe tieto geometrické entity sa vyznačujú veľkosťou špecifickou pre ich priestor, definovanou maximálnym počtom dostupných rozmerov. Najskôr plocha (2D) pre obdĺžnik a objem (3D) pre obdĺžnik - veličiny, ktoré určujú, koľko priestoru entity skutočne zaberajú. Potom veľkosť nevhodná pre tento priestor, definovaná počtom dimenzií o jednotku menšou ako je tento priestor, veľkosť, ktorá predstavuje entitu, ktorá geometricky „uzavrie“ dané telo: obvod (1D) v prípade obdĺžnika, respektíve bočná plocha (2D ) v prípade rovnobežnostenca.

S predĺžením bude hyperparalleipiped definovaný a hipervolum (4D) a a bočný objem (3D) predstavované súčtom objemov rovnobežnostenov na jeho končatinách. Pretože ak je obdĺžnik uzavretý segmentmi a štvorhran uzavretý obdĺžnikmi, hyperparalleipiped bude uzavretý rovnobežnostenmi, že? Presne tých 8, ktoré ste identifikovali o niečo skôr.

Na úvod uveďme zoznam známych geometrických vzorcov.

Po intuitívnom stanovení vzorcov 2D a 3D, hľadaní pravidla a jeho rozšírení na 4D, budeme v pokušení veriť tomu, že:

Toto sú overené vzorce pre predchádzajúce dva prípady. Pre bočný objem hyperparalelipipedu nie je nutná žiadna demonštrácia, jednoduché sledovanie rovnobežnostenov na jeho koncoch, ktorých výpočtové vzorce pre objem poznáme, postačujúce na pozorovanie správnosti intuície.

Pre hyperpriestor sa na preukázanie vzorca môže použiť integrálna metóda výpočtu. Analogicky s výpočtom plochy jednoduchým integrálom, respektíve výpočtom objemu dvojitým integrálom, sa stanovenie hypervolumu uskutoční pomocou trojitého integrálu, ako je uvedené nižšie. Aj keď sa v trojnásobnej integrálnej matematike podľa objemu zvyčajne prijíma, že predstavuje „hustotu“, štvrtá fyzikálna dimenzia ju môže charakterizovať ešte lepšie.

Pretože sme vybrali tieto entity takým spôsobom, že obsahujú iba paralelné strany, stáva sa integrálny výpočet veľmi jednoduchým a všetky funkcie, ktoré sa majú integrovať, sú v skutočnosti konštantné:

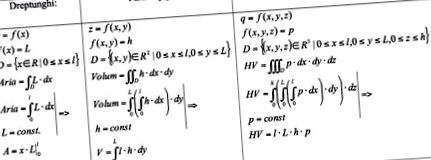
Obdĺžnikový hypertetrahedron

Teraz, keď sme zahriali našu myseľ týmto veľmi jednoduchým prípadom, pozrime sa na druhé telo, a to obdĺžnikový hypertréder. Rovnako ako v predchádzajúcom prípade budeme postupovať pozorovaním jeho vzniku, počnúc pravým trojuholníkom.

Teraz namiesto „nakreslenia“ alebo „znásobenia“ trojuholníka v rovine xy pozdĺž osi z, vezmeme bod na osi z, v určitej vzdialenosti od roviny trojuholníka, a spojíme ho so všetkými rohmi. čím sa získa obdĺžnikový štvorsten. Ako keby sme trojuholník „znásobovali“ a neustále „zmenšovali“ až ku koncovému bodu. Rovnakým spôsobom, berúc do úvahy tentokrát bod na osi q mimo priestor x-y-z a spojiac ho so štyrmi bodmi predtým získaného obdĺžnikového štvorstenu, vygenerujeme obdĺžnikový hypertréder.

A v tomto prípade pre lepšie zobrazenie môžete vytvoriť 3D model, ako je to uvedené nižšie, pričom sa vychádza z obdĺžnikového štvorstena a kreslenie hrán z každého z jeho rohov do bodu na osi q je nepravdivé kolmé na všetky ostatné. tri z xyz priestoru: môžete identifikovať štyri štvorsteny, ktoré sa objavili a ohraničiť 4D telo? Som presvedčený, že áno.

Relevantné geometrické vzorce v tomto prípade by boli:

Rovnako intuitívne, ako v predchádzajúcom prípade, nájdeme:

Opäť platí, že vzorce, ktoré sa osvedčia v 2D a 3D.

Bočný objem je opäť relatívne ľahko dokázateľný, a to podľa obrázka a identifikácie štyroch objemov obdĺžnikového štvorstena, ktorého vzorce poznáme, plus objem základného štvorstena, vypočítaný pomocou rozšírenej vety De Gua. A demonštrácia trojnásobnou integráciou objemu pre hypervolume hypertretédera je nasledovná (tu sa veci trochu komplikujú, pretože integračné funkcie, aj keď sú lineárne, už nie sú konštantné, ale všetky klesajú s určitým sklonom):

Pre ešte lepšiu vizualizáciu, podobnú procesu, pri ktorom sa trojrozmerné teleso premieta do troch rovín, čím sa dosiahne znázornenie v „čírom“, a štvorrozmerné telesá je možné navrhnúť v štyroch 3D priestoroch, ako je uvedené nižšie, pričom sa získa teda „pohľad“ v každom zo štyroch zložkových priestorov hyperpriestoru na študovanú hyperbody:

Ako vás vyzývam, aby ste modelovali, kreslili a analyzovali ďalšie štvorrozmerné telá. A ak sa pýtate, prečo by bolo zaujímavé mať vizuálnu reprezentáciu abstraktných telies definovaných vo viacerých dimenziách ako konkrétny svet, povedzme to len preto, že nemôžeme vedieť, kedy a ako nás zložitejšie svety vyzvú, aby sme ich preskúmali.